Basics: Moment of inertia

Matthias Beetz, Baumüller Nürnberg GmbH

Read min.

The moment of inertia is the force that counteracts the change in angular speed. It must be overcome to achieve a rotational movement. Apart from a vacuum, energy must always be expended to generate or maintain movement. This also applies to rotations. In the practical application case of a motor, the moment of inertia counteracts the torque of the rotor.

The following glossary entry deals with:

Index

Designation and definition of term

The moment part of the work indicates a rotational movement. Inertia refers to Newton’s first law of motion, the law of inertia. It describes that a body at rest remains at rest unless it is acted on by a force. The moment of inertia could thus be called the antagonist of torque, so to speak. In practice, this should cause a body to rotate about an axis, while the moment of inertia is a variable that has to be overcome.

Alternative, commonly used terms are also:

Rotational inertia, Second moment of mass
Mass moment of inertia
Angular mass

Basics: Newton’s laws of motion

Above all, Newton’s first and second laws of motion are relevant for understanding the moment of inertia. According to the law of inertia, bodies remain at rest, i.e. do not move if no forces act on them. The second law describes the principle of action. Accordingly a body is accelerated if a force acts on it.

The (net) force is the product of mass and the acceleration effect.

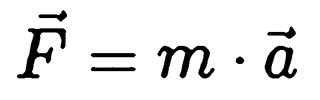
However, this only applies to a vacuum. Due to the Earth’s gravitation, the mass of a body counteracts the rotational force.

Calculating the moment of inertia

The standard formula is:

J = m x r²

J – moment of inertia
m – mass
r – distance from the axis of rotation

The moment of inertia therefore results on the one hand from the mass to be moved and the square of the length of the rotational arm. However, this is only the moment of inertia of an individual mass point. In practice a volume integral must be used to take into consideration the body's mass distribution.

Composition of the moment of inertia

In relation to a drive, the moment of inertia is a collective term. This is because moments of inertia are created in different places. They must be overcome collectively to generate the rotation. This includes all parts that are to be made to rotate. This can be clearly illustrated using the example of a ship’s propeller. In the motor itself, the rotor has a moment of inertia. In addition, there are the moments of inertia of all other rotating parts of the drive, the gear ratio and of course the parts to be driven – in this case the ship’s propeller. In addition, in practice there are ultimately also friction resistances, as well as the force that is needed to move the water.

Interaction with other forces

Numerous forces act in the drive. The moment of inertia, which results from the mass of the components and all parts to be moved with the drive, is only one factor, which has to be overcome to increase the angular speed in the system. In addition there are also friction resistances. The torque must overcome all these forces in order to get the rotor of the drive to rotate and to accelerate.

The moment of inertia in drive technology

In drive building practice at Baumüller the moment of inertia must always be taken into consideration. There are also starting points for optimization. As, in simple terms, the moment of inertia is the product of the mass and radius, it is possible to start with these two points. On the one hand, lightweight construction methods can be used to reduce the mass of rotating components. On the other hand, a compact design can reduce the radius of rotation. Both compact and lightweight construction methods are our specialty, which enables us to highly optimize the moment of inertia. Therefore, energy can be saved in operation and costs can be lowered.

Summary

The moment of inertia is a physical variable that results from the Earth’s gravitational force. It results when mass points rotate about an axis and has to be overcome to achieve an increase in the angular speed. According to Newton’s 1st law of motion, bodies “want” to remain at rest – which results in practice from the mass of a body – which consequently also means a corresponding weight has to be moved. A simplified calculation of the moment of inertia is the product of the mass times the radius of the rotor arm.

Do you have any questions?

Matthias Beetz
Training Engineer Academy I Baumüller Nürnberg GmbH

Our experts will be happy to help you.

Do you have any questions?

Please describe your request

Company and contact person

Salutation

Mr. Ms. Invalid Input

First Name

Please fill in first name

Last Name*

Please fill in last name

lastname

Invalid Input

Company*

Please fill in the company name

Country*

Please select a country

Street, Number

Please provide a street and number

Zip Code*

Please fill in zip code

City*

Invalid Input

Please indicate your company location so that we can find the right contact person for your region.

How would you like to be contacted?

by phone by e-mail Bitte geben Sie an, wie wir Sie kontaktieren sollen.

Email*

Private email domains are excluded

Country Code

Invalid Input

Phone

Invalid Input

completePhone

Invalid Input

Antispam*

Invalid Input

The fields marked with an asterisk (*) are mandatory.